Daily Puzzles
The Broken Chessboard Riddle
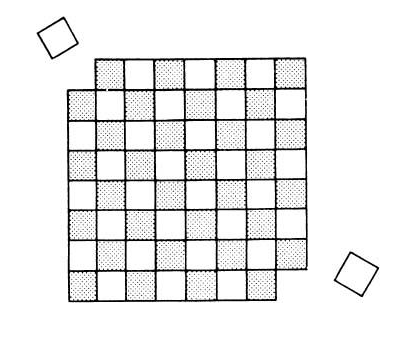
You have a chessboard and 32 dominoes. Each domino can cover two adjacent squares on the chessboard. Therefore, the 32 dominoes can cover all 64 squares on the board. If you cut out two squares at diagonally opposite corners of the chessboard and throw out one of the dominoes, is it possible to arrange the 31 dominoes on the board so that the 62 remaining squares are covered? Explain.
It is not possible. Explain why.
No. Each domino covers two adjacent squares with opposite colors. The diagonally opposite squares that were removed from the board are of the same color. This means that there are now two more squares of one color than the other. If you try rearranging the dominoes on the chessboard, you can cover 60 squares with 30 dominoes, but you will be left with two uncovered squares of the same color. Squares of the same color cannot be adjacent, so they cannot be covered by the remaining domino.