Brother vs. Sister

John has two siblings, a brother and a sister, whom he both loves very much. Every Saturday, he takes the subway to visit one of them. To visit his brother, John takes a train on the downtown side of the platform. To visit his sister, he takes a train on the uptown side of the platform. He likes both his siblings equally well, so he simply takes whichever train first comes along. He arrives at the platform at a random time each Saturday. Both trains arrive at the station equally often – every 10 minutes. However, John realized that he has been spending more time with his brother than his sister (9 times out of 10). Why do the odds favor John's brother so much?
Consider John's waiting time for each train.
Even though the trains arrive equally often at 10 minute intervals and John arrives at a random time, the train schedules are such that the train to his sister arrives one minute after the train to his brother. Therefore, the train to see John's sister will only come first if John arrives during that one minute interval. If John arrives during the 9 minute interval, he will get on the train to see his brother. So the odds are nine to one.

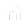 Daily Puzzles
Daily Puzzles